Digital PSAT Math Practice Question 75: Answer and Explanation

Question: 75

If -2| -3| < -3|x + 5|, what are all possible values of x?

• A. -7 < x < -3
• B. -3 < x OR -7 > x
• C. -3 < x
• D. No solutions

Correct Answer: A

Explanation:

(A) Let's start with the left side of the inequality. The absolute value of -3 is 3, so:

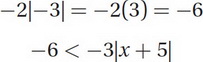
We want to isolate our absolute value. So let's divide by -3, flipping the inequality since we are dividing by a negative number:

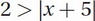
Because 2 has to be greater than the absolute value, the expression inside of the absolute value symbol can be anything between (-2, 2). In other words, x - 5 needs to be greater than -2 but less than 2. To find the x-values such that x - 5 is less than 2, simply take away the absolute value signs and solve for x:

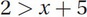
Subtracting 5 from both sides gives:

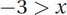
Next, we want to find the values of x such that x - 5 is greater than -2. In other words, we want to solve for x in the inequality -2 < x + 5. Subtracting 5 tells us:

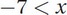
We have found that -3 > x and that -7 < x. In other words, -7 < x < -3, which is choice (A).