Digital PSAT Math Practice Question 68: Answer and Explanation

Question: 68

If Equation A is defined by 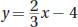and if Equation B is defined by 3y = 2x + 3, what must be done to Equation B so that the system of both Equation A and Equation B will have infinitely many solutions?

• A. Add 9 to the right side
• B. Subtract 5 from the right side
• C. Subtract 7 from the right side
• D. Subtract 15 from the right side

Correct Answer: D

Explanation:

(D) First, you must consider how two lines could have infinitely many solutions. The answer is that they need to have the same slope and the same y-intercept. In other words, they are the same line when graphed.

Let's start by rewriting Equation B in slope-intercept form by dividing both sides by 3:

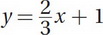
The equations already have the same slope. However, they also need to have the same y-intercept: -4.

Let's subtract 5 from the right side of Equation B so that it matches Equation A:

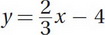
However, we want to know what we need to change about the original Equation B. Therefore, we want to get Equation B back in its original form to see what changed. We can do this by multiplying both sides by 3:

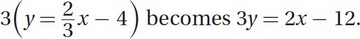
Now we can see that from Equation B to this final equation, we subtracted 15 from the right side to change the y-intercept from +3 to -12. This matches choice (D).