Digital PSAT Math Practice Question 302: Answer and Explanation

Question: 302

The formula for the compound interest on a monetary investment is 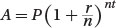in which the variables stand for the following quantities:

A is the total amount of money after n years, including accumulated interest.

P is the principal amount (i.e., the initial amount invested).

r is the annual interest rate expressed as a decimal (e.g., 3% interest is expressed as 0.03).

n is the number of times per year that the interest is compounded.

t is the number of years the money is invested.

Linda invests $10,000 in a bond fund. Her investment advisor told her that the fund earns 10% compounded a year, but the adviser failed to tell her whether the interest is compounded each month or just once per year. How much more interest in the first year of the investment would she earn if the interest on the fund is compounded monthly versus compounded annually (enter your answer to the nearest whole dollar, omitting the dollar sign)?

Correct Answer: 47

Explanation:

47 In both cases, P = 10,000, r = 0.10, and t = 1. If interest is compounded yearly, n = 1, whereas if it is compounded monthly, n = 12. Because she starts with $10,000 either way, the difference in (A) in the two situations can only be the result of differing amounts of interest. Therefore, you can figure out how much money she would have if it were compounded monthly and subtract the amount of money she would have if it were compounded annually in order to determine how much more interest she would earn in the monthly scenario.

Monthly:

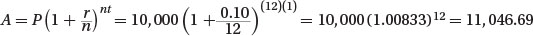
Yearly:

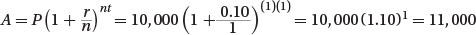
Therefore, the difference in the amount of interest earned in the two scenarios is given by the difference 11046.69 - 11000 = 46.69. Rounded to the nearest dollar, $47.