Digital PSAT Math Practice Question 290: Answer and Explanation

Question: 290

In what quadrants of the xy-coordinate plane will solutions to y > |x| + 1 be found?

• A. First only
• B. Fourth only
• C. First and second only
• D. Third and fourth only

Correct Answer: C

Explanation:

(C) To solve this problem, first assess the domain and the range of |x| + 1. Any value can be plugged into the equation for x, so the domain will be all real numbers.

Next, consider the range. Remember that the absolute value of a number is that number's distance from zero. Since it is a distance, the absolute value of any number must necessarily be nonnegative (i.e., |x| ≥ 0). Thus, |x| + 1 ≥ 0 + 1 = 1, so the range is [1, ∞).

This domain and range correspond to a function in the first and second quadrants.

However, notice that the problem is an inequality rather than a function. Therefore, you need to also assess what part will be shaded. The inequality says that y will be greater than the value given by the expression on the right, which means the area above the graph of |x| + 1 will be shaded. Therefore, your original answer of the first and second quadrants is valid.

Alternatively, consider this problem graphically: |x| + 1 shifts the graph of |x| up by 1, so the graph looks like

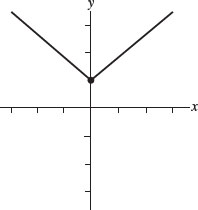
You want y to be greater than |x| + 1, so y can only take values in the region above the graph, which is shaded in the picture below:

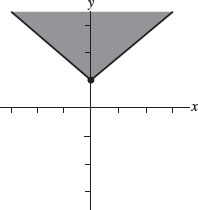
Thus, points (x, y) satisfying the inequality can only be found in the first and second quadrants.