Digital PSAT Math Practice Question 280: Answer and Explanation

Question: 280

Consider a rectangular prism with a height of A, a length of B, and a width of C. How many pyramids of the same length and width of this prism, but half its height, can fit into the prism?

Correct Answer: 6

Explanation:

6 You are given the formula for the volume of a rectangular prism, V_r = lwh, at the beginning of the math section. In this problem, your rectangular prism has height A, length B, and width C, so the formula becomes V_r = BCA. You want to know how many pyramids with the same length and width of the prism, but half of its height, can fit into the prism. You are also given the formula for the volume of a pyramid, 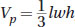, at the beginning of the math section. Since the pyramids have the same length and width as the prism, l = B and w = C. The height is half of the prism, so 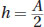. Thus, each pyramid has volume . Note that . 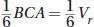Therefore, since 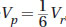, it follows that 6 V_p = V_r. In other words, you can fit 6 pyramids into the rectangular prism.