Digital PSAT Math Practice Question 249: Answer and Explanation

Question: 249

Jasmine has $100,000 in an investment portfolio, divided among only the categories of stocks, bonds, and cash. She has twice as much invested in stocks as she does in bonds, and three times as much invested in bonds as she has in cash. What percent of her portfolio is invested in bonds?

• A. 22%
• B. 27%
• C. 30%
• D. 44%

Correct Answer: C

Explanation:

(C) Create a system of equations. First, you know that she has $100,000 invested among the three categories, so if s, b, and c represent the amount of money in stocks, bonds, and cash respectively, then s + b + c = 100, 000.

She has invested twice as much in stocks as in in bonds, so s = 2b.

She has invested three times as much in bonds as in cash, so b = 3c.

The question asks how much money is invested in bonds, so you want to get s and c in terms of b, plug these expressions into the first equation, and solve for b. The second equation is already solved for s in terms of b, but you need to solve the third equation for c in terms of b:

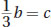. Next, plug these expressions in for s and c in the first equation:

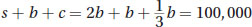. You can combine like terms to get

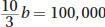. Divide both sides by 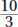to get b = 30,000. The question asks what percent is invested in bonds, so find what fraction 30,000 is of 100,000, and multiply that number by 100%:

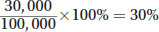, answer (C).

Alternatively, you can figure out the ratio of the investments:

Cash: Bonds: Stocks = 1 : 3 : 6

The total of the numbers in this ratio is 1 + 3 + 6 = 10.

Therefore, as fractions of the whole, the investments are 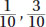, and .

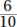The bonds are 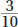, which translates to 30%.