Digital PSAT Math Practice Question 241: Answer and Explanation

Question: 241

What is the x coordinate of the minimum of the parabola with the equation y + 17 = 6x² + 12x?

• A. -1
• B. 0
• C. 2
• D. 3

Correct Answer: A

Explanation:

(A) First, get the equation into standard form by subtracting 17 from both sides: y = 6x² + 12x - 17. When a parabola is in standard form, y = a x² + bx + c, the axis of symmetry is given by the equation . Because the axis of symmetry passes through the vertex and this parabola opens up, the x value that gives the axis of symmetry will also give the x coordinate of the vertex. The y and x values of the vertex give the minimum value and its location on the parabola, respectively, so you want to know the x value of the vertex to solve this problem.

In this case, a = 6 and b = 12, so 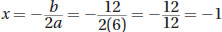. This corresponds to answer (A).

Alternatively, you could have converted the equation to vertex form by completing the square to get: y = 6(x + 1)² - 17. Then the vertex is (-1,-23), so x = -1.