Digital PSAT Math Practice Question 153: Answer and Explanation

Question: 153

A train is traveling for 5 hours at a constant rate of x miles per hour and then travels an additional 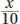hours at a speed of 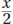miles per hour. If the train travels a total of 300 miles during these two segments, which equation could be used to solve for x?

• A. x² + 100x - 6,000 = 0
• B. x² + 100x - 300 = 0
• C. x² + 5x - 300 = 0
• D. 3x² +150x - 6,000 = 0

Correct Answer: A

Explanation:

(A) Remember that d = rt, where d is distance, r is rate, and t is time. We have two different rates and two different times. We can multiply the coinciding rates and times together and then can add them to obtain the total distance traveled, 300 miles:

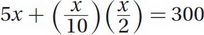
Multiplying the two fractions together leaves:

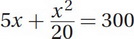
None of the answer choices has a denominator, so let's multiply both sides by 20 to get rid of the denominator:

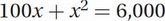
Subtracting 6,000 from both sides and rearranging the terms gives:

This matches choice (A).