Digital PSAT Math Practice Question 112: Answer and Explanation

Question: 112

equals which of the following, given that a ≠ ±b ?

• A. a + b
• B. a - b
• C. a²b - ab²
• D. a² + b²

Correct Answer: A

Explanation:

(A) From all of the answer choices, we can see that the whole denominator cancels out somehow. Let's use polynomial long division to figure out an equivalent expression for our original fraction. Before we use long division, let's first combine like terms in the numerator so that the long division isn't as complicated:

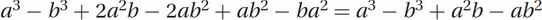
Now do polynomial long division:

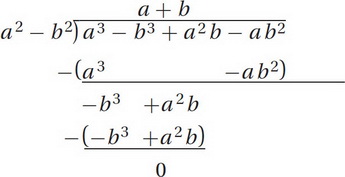
Thus, our original fraction is equal to a + b, which is choice (A).

Alternatively, you could have simplified directly by factoring. Since a³ - b³ = (a - b)(a² + ab + b²), we can rewrite the numerator:

a³ - b³ + 2a²b - 2ab² + ab² - ba² = a³ - b³ + a²b - ab² = (a - b)(a² + ab + b²) + a²b - ab²

Notice that a²b - ab² = ab(a - b), so our numerator becomes:

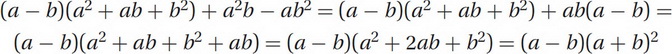
Thus, our original fraction can be rewritten as 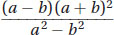. Since our denominator is a difference of squares, it can be rewritten as a² - b² = (a + b)(a - b). Our entire expression becomes:

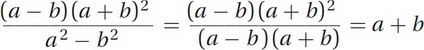
Choice (A) is correct.